Hyperpolarization recovery

동현님이 올려주신 comment를 보고 생각을 해보다가 Membrane voltage를 직접 그려봐야겠다는 생각을 해보았다.

(특히 이 부분 "This is because membrane potential changes are not determined by concentration changes, but by permeability changes." 사실 처음 이 부분을 보았을때 동의할 수 없었다. 왜냐하면 permeability 변화로 인해 ion concentration이 변화해서 결론적으로 membrane potential 이 변할꺼 같다고 생각했기 때문이다.)

이 상황에는 Nernst equation보다 Goldman equation이 더 적절하고, K+ 와 Na+ 만 고려해도 큰 상관이 없다고 판단하였다.

Goldman equation

$$\begin{align} V_{m} &= {RT \over F} \,\, log \left({{P_k [K^+]_{out} +P_{Na} [Na^+ ]_{out}} \over {P_k [K^+]_{in} +P_{Na} [Na^+ ]_{in}}} \right) \\ &= 61.54mV \,\, log_{10} \left({{P_k [K^+]_{out} +P_{Na} [Na^+ ]_{out}} \over {P_k [K^+]_{in} +P_{Na} [Na^+ ]_{in}}} \right) \end{align}$$

Goldman equation derivation 은 다음 링크에 잘 나와있다.

Derivation of the Goldman Equation

Click on the book chapter title to read more.

https://onlinelibrary.wiley.com/doi/pdf/10.1002/9781118687864.app2

가정1) K+, Na+ ion 외부,내부 농도 고정

아주 적은 ion 들이 옮겨 간다고 알려져있고 wiki(Membrane potential) 에서도 아래와 같이 comment 되어 있어서 편의성을 위해 이렇게 가정해보았다.

(Although the membrane potential changes about 100 mV during an action potential, the concentrations of ions inside and outside the cell do not change significantly. They remain close to their respective concentrations when then membrane is at resting potential.)

가정2) P_K, P_Na 는 normal distribution 가정.

적절한 수치 데이터를 찾지 못해서, 참조(1) 그래프 개형에 맞도록 맞춰주었다.

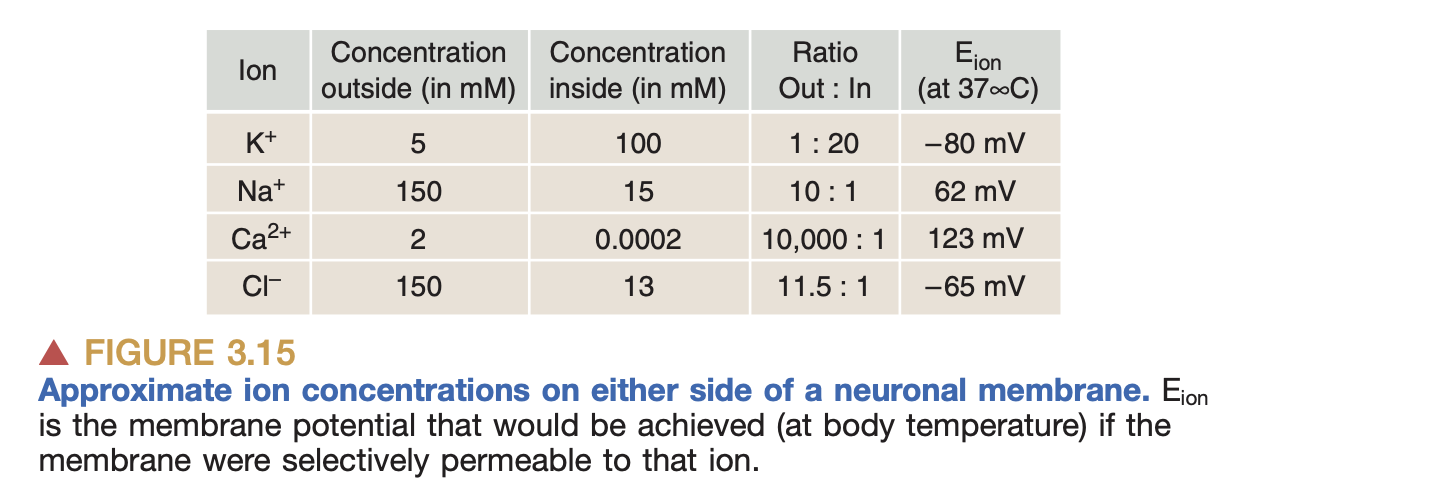
K+, Na+ 이온 농도는 neuroscience 교과서 수치를 대입하고, goldman equation 으로 membrane voltage 를 plot 하였더니 아래 그래프 처럼 그려졌다.

Permeability 만으로 hyperpolarization 및 recovery가 되는 것을 볼 수 있다.

즉, ion channel dynamics 만으로 hyperpolarization, recovery 가 된다.

• 그런데 왜 ion pump가 recovery 하는데 역할은 한다고 하는 이유는 뭘까?

goldman equation에서 total flux (current 라고 생각해도됌) = 0 으로 가정해서 식을 전개해나간다.

하지만 실제로 total flux 는 0이 아니다. Na+, K+ ion 의 flux가 생기는데 이를 ion pump (+ active transporter) 가 대략적으로 flux를 0으로 만들어 준다. 따라서 goldman equation의 가정을 맞도록 해줘서 recovery 역할을 한다고 언급되는거라 생각된다.

아래는 goldman equation wikipedia 에 나온 내용이다.

(Although the current for each ion type considered here is nonzero, there are other pumps in the membrane, e.g. Na+/K+-ATPase, not considered here which serve to balance each individual ion's current, so that the ion concentrations on either side of the membrane do not change over time in equilibrium.)

(P.S. +hodgkin huxley model에서 permeability 관련해서 다루는데 그런 점에서 생각해보면 hyperpolarization 및 recovery는 당연한거 같기도하다....)

(참조1)

Important Features of the Neuronal Action Potential - Neuronal Action Potential - PhysiologyWeb

This lecture describes the details of the neuronal action potential. The lecture starts by describing the electrical properties of non-excitable cells as well as excitable cells such as neurons. Then sodium and potassium permeability properties of the neuronal plasma membrane as well as their changes in response to alterations in the membrane potential are used to convey the details of the neuronal action potential.

https://www.physiologyweb.com/lecture_notes/neuronal_action_potential/neuronal_action_potential_important_features.html

(참조2) - Mark F. Bear PhD, Barry W. Connors PhD, Michael A. Paradiso PhD-Neuroscience_ Exploring the Brain

(plot code)

import numpy as np
import matplotlib.pyplot as plt

#P_K : P_Na = 40 : 1
#mM
K_ion_out = 5
Na_ion_out = 150
#K_ion_in
#Na_ion_in

def goldman_vm(K_ion_in,Na_ion_in,P_K,P_Na):
    vm = 61.54 * np.log10((P_K * K_ion_out + P_Na * Na_ion_out) / 
                          (P_K * K_ion_in + P_Na * Na_ion_in))

    return vm


def normal_dist(x,mu,sigma):
    y = (1 / np.sqrt(2 * np.pi * sigma**2)) * np.exp(-(x-mu)**2 / (2 * sigma**2))

    return y

## 끼워맞추기 ##
fig,ax = plt.subplots(1,1,figsize=(12,10))

x = np.linspace(-1,5,1200)
P_Na_array = 40*normal_dist(x,1,0.2)+1/6
P_K_array = 40*normal_dist(x,1.5,0.3)+40/6
vm = goldman_vm(100,15,P_K_array,P_Na_array)

ax.plot(x,P_Na_array-80,linewidth=4,c='darkred',label='P_Na')
ax.plot(x,P_K_array-80,linewidth=4,c='darkcyan',label='P_K')
ax.plot(x,vm,linewidth=4,c='blue',label='Vm')

ax.set_title('Goldman equation plot', fontsize=25)
ax.set_ylabel('Voltage (mV)',fontsize=16)
ax.set_xlabel('Time (ms)',fontsize=16)
ax.tick_params(axis='both', labelsize=16)
ax.legend(loc='upper right',prop={'size':20})

Uploaded by N2T